Testing

Relevant Tests

Unit Tests
• Unit tests apply to code at the method level
• Quickly access and test a part of the business logic
• Useful for test-driven-development

Integration Tests
• Combined modules tested as a whole
• Performed after modules are unit tested

Validation Tests
• Checking if the system satisfies its requirements

Unit Testing

First and foremost, we decided that a project of this length would increasingly evolve over time, and would naturally need to adapt to unpredictable events. If steps are not taken to manage these changes, there can arise problems between new and old functionality, such that initial classes no longer behave as you might expect them to. To ensure that every iteration was aware of any side-effects, we chose to unit test our core class methods, and in the process guarantee that past commits were never overshadowed or forgotten about.

System Specific

Our immediate concerns, regarding testing, can be broken into two parts:

• Reliability (i.e. consistency between scans)
• Accuracy (i.e. noise measurement, outlier removal)

Reliability
With regards to consistency between scans: confidence in the scanner’s ability to deliver similar results from consecutive scans was critical. In order to provide evidence of the system’s reliability, we requisitioned a human body mannequin with the intention of using it as a completely static model for the scanning process.

We took 200 consecutive scans of the mannequin, outputting point clouds for each scan. We found that the marginal differences between the corresponding points’ (x,y,z) values were often less than 5 millimetres, meaning the scans were very similar and, indeed, rendered almost identically in MeshLab.

In the process of this experiment, we did discover details of how we would best prepare the environment surrounding the model during the scan.

For best results:

• Reduce or remove all floor clutter
• Avoid standing close to objects such as desks, chairs etc.
• Stand at least a few feet in front of a, contrasting in colour, background surface

Accuracy
For accuracy, we want to remove as much noise from the scan as possible. To do so we can try to filter outliers by performing a Nearest Neighbour Search on each of the point cloud’s points, identifying the closest N points before averaging their distances.

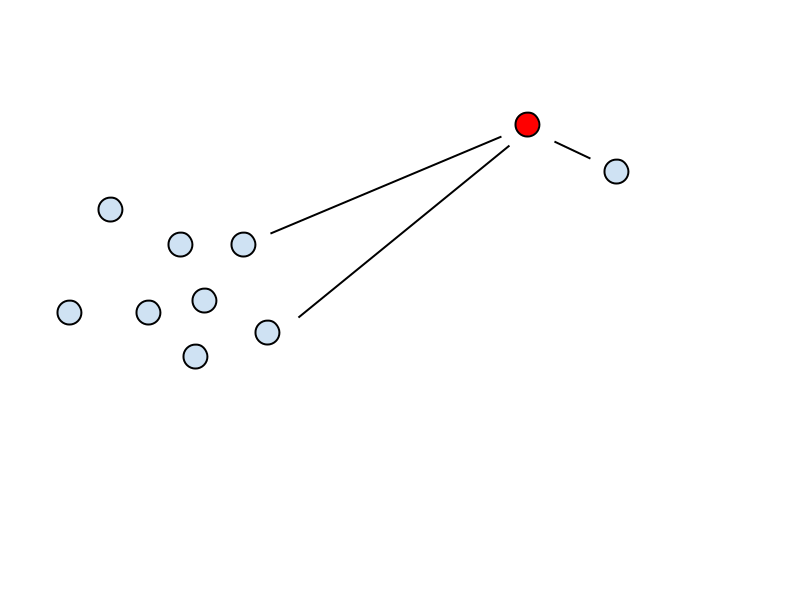
Outliers will tend to have larger average distances to their closest points when compared to connected points that are tightly grouped. By thresholding this average distance value, we can successfully remove dramatic outliers.

For performance and ease, we will store the 3D points in a k-d tree, alternating splitting with hyperplanes across the x, y and z axis. This allows for efficient NN search by creating the invariant that all points in the left subtree of node A must have a lower axis value than A itself, while all those in the right subtree must have a higher value for that axis.