Forces and Gravity

In this lesson, we are going to learn about physics! We are going to look into how the rocket propels forward and the forces that cause the motions.

There are 2 forces that are acting on the rocket:

• Gravity
• Thrust of the engine

We can understand this through push and pull concept - the gravity is pulling the rocket towards the ground, while the thrust, created by the burning of the fuel, acts as the push to keep the rocket in the direction it is pointing in.

Newton Laws of Motion

First law

The Newton’s first law of motion, which is also known as the law of inertia, states that an object at rest will always stay at rest and an object in motion will always stay in motion with the same speed and in the same direction unless acted upon by an external force. It applies to the rocket as well. Do you ever wonder why the rocket will fall without the thrust and will keep falling until it reaches the ground? This is because there is an external force, the gravity, that acts on the rocket. Gravity is the unbalanced force in this case that forces the rockets to move and accelerate towards the ground until it crashes. When the rocket crashes, the gravitational force will be balanced by normal reaction. Hence, the rocket will stay stationary until it is moves by an external force again.

Second law

According to the Newton’s second law of motion, the acceleration of an object is directly proportional to the magnitude of the net force producing it, and the direction of the acceleration is in the same direction as the net force. It is also inversely proportional to the mass of the object.

In the lunar lander, the acceleration of the rocket is determined by the ratio between the thrust and the weight. In this case, Weight = mg, where g = gravity. It will be further explained as the tutorial goes on.

Third law

Formally stated, Newton's third law is:

For every action, there is an equal and opposite reaction.

The statement means that in every interaction, there is a pair of forces acting on the two interacting objects. The size of the forces on the first object equals the size of the force on the second object.

In this case, it’s the force created by expelling the matters of the fuel away from the rocket and the reaction force created while doing so. While the emitting force is acting downwards, the reaction force is acting upwards, hence providing an upthrust or a lift on the rocket to overcome the weight.

There are 3 cases for the up and down motions:

1. Upthrust > Weight: The rocket moves upwards. The more fuel the rocket burns, the bigger the upthrust, and hence the faster the rocket moves upwards.

2. Upthrust = Weight: The rocket stays stationary. The upthrust and weight equalize each other. So, there is no net force acting on the rocket, which leads to no motion.

3. Upthrust (or no upthrust) < Weight: The rocket falls (towards the ground) due to the gravitational force acting on the mass of the rocket.

Forces at an angle

When the rocket moves to left and right, the mechanism is distinct to the sole up and down movements because the forces are not only acting upwards or downwards, they are also acting to either the left or the right. The net force acts on certain angle to the vertical.

There are 4 cases:

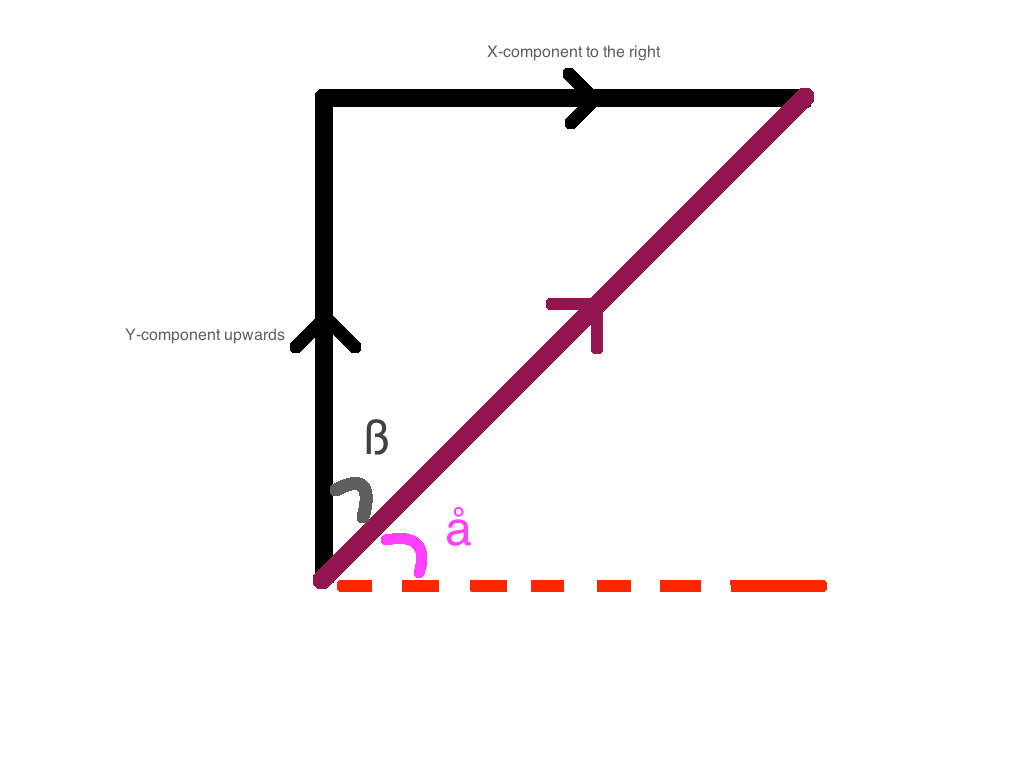
1. Up and Right: The net y-component of the force is upwards. The net x-component of the force is to the right. The resultant component of the force will be at angle ß to the vertical.

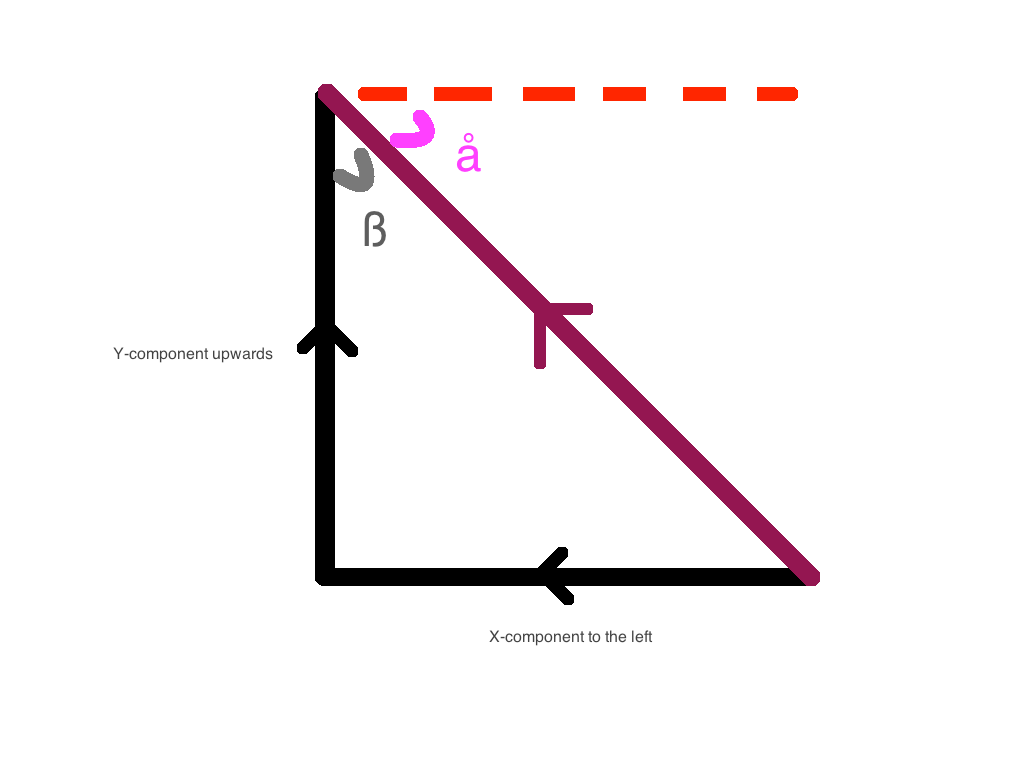
1. Up and Left: The net y-component of the force is upwards. The net x-component of the force is to the left.

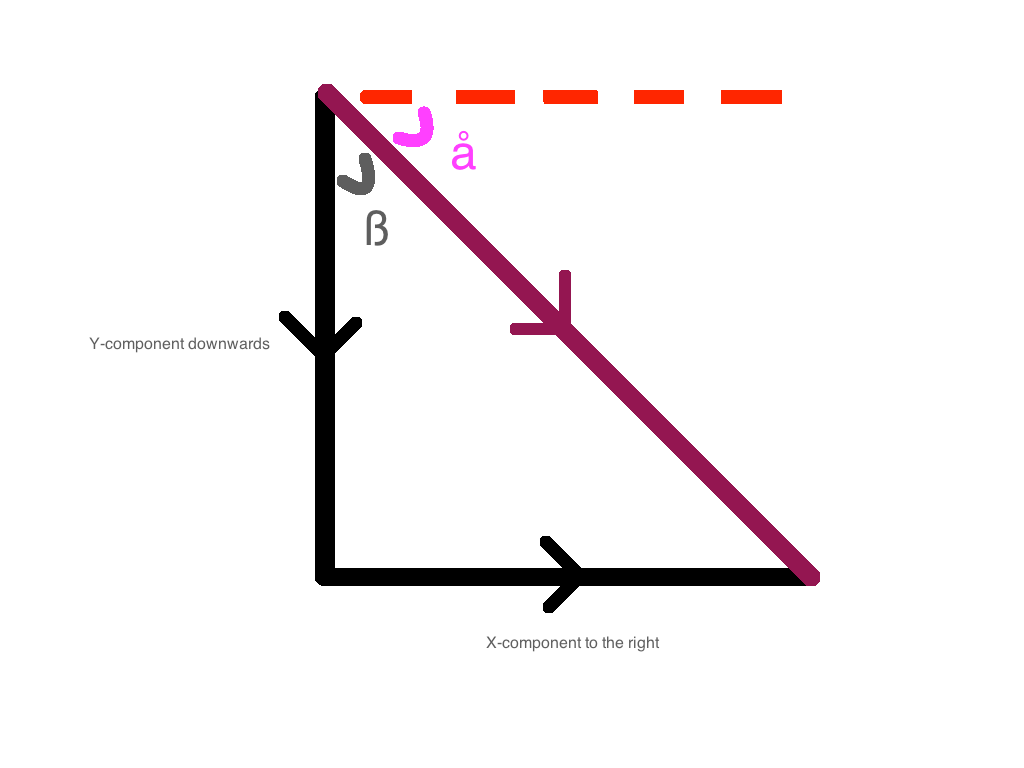
1. Down and Right: The net y-component of the force is downwards. The net x-component of the force is to the right.

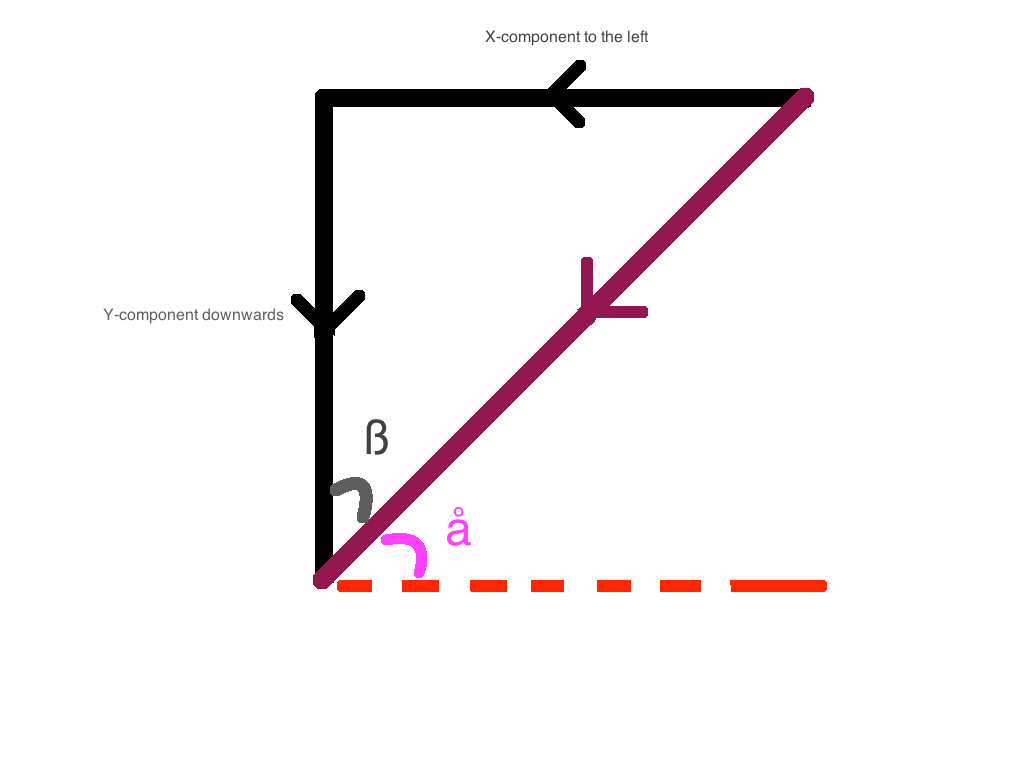
1. Down and Left: The net y-component of the force is downwards. The net x-component of the force is to the left.

What if you net force component and wish to calculate the x-component and y-component respectively?

Simple, you can do that using trigonometry:

where

$F$ is the net force

$F_x$ is the x-component of the force

$F_y$ is the y-component of the force

$\theta$ is the angle to the upward vertical

Applying the theory

In order to implement first law, we need to keep track of the current velocity of the spaceship. So let's add a property called velocity:

var spaceship =
{
    color: "black",
    width: 8,
    height: 22,
    position:
    {
        x: 0,
        y: 0
    },
    angle: 0,
  velocity: {
    x: 0,
    y: 0
  },
    engineOn: false,
    rotatingLeft: false,
    rotatingRight: false,
}

Let's also change our updateSpaceship() function to increment/decrement x and y coordinates based on the current velocity:

function updateSpaceship()
{
    spaceship.position.x += spaceship.velocity.x;
    spaceship.position.y += spaceship.velocity.y;
    if(spaceship.rotatingRight)
    {
        spaceship.angle += Math.PI / 180;
    }
    else if(spaceship.rotatingLeft)
    {
        spaceship.angle -= Math.PI / 180;
    }

    if(spaceship.engineOn)
    {
        // these will change as we now implement forces
        // spaceship.position.x += Math.sin(spaceship.angle);
        // spaceship.position.y -= Math.cos(spaceship.angle);
    }
}

Note that the velocity also needs to be updated when there is a force acting on the spaceship. And there is always a force (or two) acting on the spaceship, so the velocity will constantly update.

As gravity acts downwards along the y coordinate, we need to keep decreasing the y velocity due to gravity:

var gravity = 0.1;

function updateSpaceship()
{
    spaceship.position.x += spaceship.velocity.x;
    spaceship.position.y += spaceship.velocity.y;
    if(spaceship.rotatingRight)
    {
        spaceship.angle += Math.PI / 180;
    }
    else if(spaceship.rotatingLeft)
    {
        spaceship.angle -= Math.PI / 180;
    }

    if(spaceship.engineOn)
    {
        // we will update this in the next code example
    }
    spaceship.velocity.y -= gravity;
}

Additionally, when there is thrust, we would like to change the velocities:

var gravity = 0.1;

function updateSpaceship()
{
    spaceship.position.x += spaceship.velocity.x;
    spaceship.position.y += spaceship.velocity.y;
    if(spaceship.rotatingRight)
    {
        spaceship.angle += Math.PI / 180;
    }
    else if(spaceship.rotatingLeft)
    {
        spaceship.angle -= Math.PI / 180;
    }

    if(spaceship.engineOn)
    {
        spaceship.velocity.x += spaceship.thrust * Math.sin(-spaceship.angle);
        spaceship.velocity.y += spaceship.thrust * Math.cos(spaceship.angle);
    }
    spaceship.velocity.y -= gravity;
}

That's enough to be able to fly the spaceship!